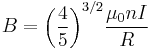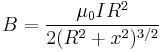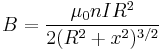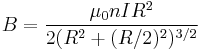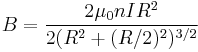Helmholtz coil

A Helmholtz coil is a device for producing a region of nearly uniform magnetic field. It is named in honor of the German physicist Hermann von Helmholtz.

Contents

Description

A Helmholtz pair consists of two identical circular magnetic coils that are placed symmetrically one on each side of the experimental area along a common axis, and separated by a distance h equal to the radius R of the coil. Each coil carries an equal electrical current flowing in the same direction.

Setting 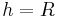h=R, which is what defines a Helmholtz pair, minimizes the nonuniformity of the field at the center of the coils, in the sense of setting 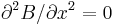\partial^{2}B/\partial x^{2} = 0[1] (meaning that the first nonzero derivative is 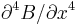\partial^{4}B/\partial x^{4} as explained below), but leaves about 7% variation in field strength between the center and the planes of the coils. 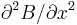A slightly larger value of h reduces the difference in field between the center and the planes of the coils, at the expense of worsening the field’s uniformity in the region near the center, as measured by \partial^{2}B/\partial x^{2}.[2]

In some applications, a Helmholtz coil is used to cancel out the Earth's magnetic field, producing a region with a magnetic field intensity much closer to zero.[3]

Mathematics

The calculation of the exact magnetic field at any point in space is mathematically complex and involves the study of Bessel functions. Things are simpler along the axis of the coil-pair, and it is convenient to think about the Taylor series expansion of the field strength as a function of x, the distance from the central point of the coil-pair along the axis. By symmetry the odd order terms in the expansion are zero. 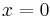By separating the coils so that charge x=0 is an inflection point for each coil separately we can guarantee that the order 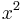x^2 term is also zero, and hence the leading non-uniform term is of order 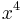x^4. One can easily show that the inflection point for a simple coil is 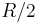R/2 from the coil center along the axis; hence the location of each coil at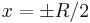 x=\pm R/2

A simple calculation gives the correct value of the field at the center point. If the radius is R, the number of turns in each coil is n and the current flowing through the coils is I, then the magnetic flux density, B at the midpoint between the coils will be given by

B = {\left ( \frac{4}{5} \right )}^{3/2} \frac{\mu_0 n I}{R}

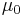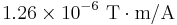\mu_0 is the permeability of free space (1.26 \times 10^{-6} \text{ T}\cdot\text{m/A}).

Derivation

Start with the formula for the on-axis field due to a single wire loop [1] (which is itself derived from the Biot-Savart law):

B = \frac{\mu_0 I R^2}{2(R^2%2Bx^2)^{3/2}}
Where:
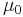\mu_0\; = the permeability constant =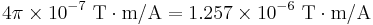 4\pi \times 10^{-7} \text{ T}\cdot\text{m/A} = 1.257 \times 10^{-6} \text{ T}\cdot\text{m/A}
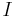I\; = coil current, in amperes
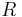R\; = coil radius, in meters
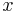x\; = coil distance, on axis, to point, in meters

However the coil consists of a number of wire loops, the total current in the coil is given by

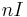nI\; = total current
Where:
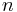n\; = number of wire loops in one coil

Adding this to the formula:

B = \frac{\mu_0 n I R^2}{2(R^2%2Bx^2)^{3/2}}

In a Helmholtz coil, a point halfway between the two loops has an x value equal to R/2, so let's perform that substitution:

B = \frac{\mu_0 n I R^2}{2(R^2%2B(R/2)^2)^{3/2}}

There are also two coils instead of one, so let's multiply the formula by 2, then simplify the formula:

B = \frac{2\mu_0 n I R^2}{2(R^2%2B(R/2)^2)^{3/2}}
B = {\left ( \frac{4}{5} \right )}^{3/2} \frac{\mu_0 n I}{R}

Maxwell coils

To improve the uniformity of the field in the space inside the coils, additional coils can be added around the outside. James Clerk Maxwell showed in 1873 that a third larger-diameter coil located midway between the two Helmholtz coils can reduce the variance of the field on the axis to zero up to the sixth derivative of position. This is sometimes called a Maxwell coil.

See also

References

  1. ^ Helmholtz Coil in CGS units
  2. ^ Electromagnetism
  3. ^ "Earth Field Magnetometer: Helmholtz coil" by Richard Wotiz 2004

External links